來源:網絡資源 2022-12-16 20:13:30
考點:寫代數式
代數式定義:由數和表示數的字母經有限次加、減、乘、除、乘方和開方等代數運算所得的式子,或含有字母的數學表達式稱為代數式。
例如:ax+2b,-2/3,b^2/26,√a+√2等。
注意
: 1、不包括等于號(=、≡)、不等號(≠、≤、≥、<、>、≮、≯)、約等號≈
2、可以有絕對值。
例如:|x|,|-2.25| 等
用運算符導(指加、減、乘、除、乘方、開方)把數或表示數的字母連接而成的式子叫做代數式。數的一切運算規律也適用于代數式。單獨的一個數或者一個字母也是代數
式,帶有“<(≤)”“>(≥)”“=”“≠”等符號的不是代數式。
分類:在實數范圍內,代數式分為有理式和無理式。
1).有理式
有理式包括整式(除數中沒有字母的有理式)和分式(除數中有字母且除數不為0的有理式)。這種代數式中對于字母只進行有限次加、減、乘、除和整數次乘方這些運算。
整式有包括單項式(數字或字母的乘積或單獨的一個數字或字母)和多項式(若干個單項式的和)
1.單項式
沒有加減運算的整式叫做單項式。
單項式的系數:單項式中的數字因數叫做單項式(或字母因數)的數字系數,簡稱系數
單項式的次數:一個單項式中,所有字母的指數的和叫做這個單項式的次數
2.多項式
幾個單項式的代數和叫做多項式;多項式中每個單項式叫做多項式的項。不含字母的項叫做常數項。
多項式的次數:多項式里,次數最高的項的次數,就是這個多項式的次數。
齊次多項式:各項次數相同的多項式叫做齊次多項式。不可約多項式:次數大于零的有理系數的多項式,不能分解為兩個次數大于零的有理數系數多項式的乘積時,稱為有理數范圍內不可約多項式。
實數范圍內不可約多項式是一次或某些二次多項式,復數范同內不可約多項式是一次多項式。對稱多項式:在多元多項式中,如果任意兩個元互相交換所得的結果都和原式相同,則稱此多項式是關于這些元的對稱多項式。同類項:多項式中含有相同的字母,并且相同字母的指數也分別相同的項叫做同類項。
2).無理式
含有 字母的根式 或 字母的非整數次乘方的代數式叫做無理式。
書寫格式:
(1)兩字母相乘、數字與字母相乘、字母與括號相乘以及括號與括號相乘時,乘號都可以省略不寫.如:“x與y的積”可以寫成“xy”;“a與2的積”應寫成“2a”,“m、n的和的2倍”應寫成“2(m+n)”。
(2)字母與數字相乘或數字與括號相乘時,乘號可省略不寫,但數字必須寫在前面.例如“x×2”要寫成”2x”,不能寫成“x2”;“長、寬分別為a、b的長方形的周長”要寫成“2(a+b)”,不能寫成“(a+b)2”。
(3)代數式中不能出現除號,相除關系要寫成分數的形式
(4)數字與數字相乘時,乘號(也可以寫作 · )仍應保留不能省略,或直接計算出結果.例如“3×7xy”不能寫成“37xy”,最好寫成“21xy”。
練習&解析
現有大小兩艘輪船,小船每天運 x噸貨物,大船比小船每天多運10噸貨物.現在讓大船完成運送100噸貨物的任務,小船完成運送80噸貨物的任務。
(1)分別寫出大船、小船完成任務用的時間?
(2)試說明哪艘輪船完成任務用的時間少?
解:(1)大船完成任務的時間為:
![]()
;
小船完成任務的時間為:
![]()
;
(2)
![]()
﹣
![]()
=
![]()
=
![]()
,
x>40時,小船所用時間少;
x=40時,兩船所用時間相同;x<40時,大船所用時間少.
考點:完全平方公式
完全平方公式是進行代數運算與變形的重要知識基礎。該知識點重點是對完全平方公式的熟記及應用,難點是對公式特征的理解 (如對公式中積的一次項系數的理解)。
兩數和(或差)的平方,等于它們的平方和,加上(或減去)它們的積的2倍,叫做完全平方公式。為了區別,我們把前者叫做兩數和的完全平方公式,后者叫做兩數差的完全平方公式。
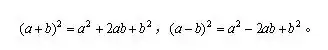
理解公式左右邊特征
(一)學會推導公式(這兩個公式是根據乘方的意義與多項式的乘法法則得到的),真實體會隨意“創造”的不正確性;
![]()
(二)學會用文字概述公式的含義:兩數和(或差)的平方,等于它們的平方和,加上(或減去)它們的積的2倍.
![]()
都叫做完全平方公式.為了區別,我們把前者叫做兩數和的完全平方公式,后者叫做兩數差的完全平方公式.
(三)這兩個公式的結構特征是:
1、
左邊是兩個相同的二項式相乘,右邊是三項式,是左邊二項式中兩項的平方和,加上或減去這兩項乘積的2倍;
2、
左邊兩項符號相同時,右邊各項全用“+”號連接;左邊兩項符號相反時,右邊平方項用“+”號連接后再“-”兩項乘積的2倍(注:這里說項時未包括其符號在內);
3、
公式中的字母可以表示具體的數(正數或負數),也可以表示單項式或多項式等數學式.
(四)兩個公式的統一:因為
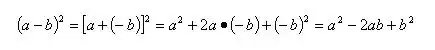
所以兩個公式實際上可以看成一個公式:兩數和的完全平方公式。這樣可以既可以防止公式的混淆又杜絕了運算符號的出錯。
練習&解析
完全平方公式的基本變形:
(一)變符號
例:運用完全平方公式計算:
(1)(-4x+3y)²
(2)(-a-b)²
分析:本例改變了公式中a、b的符號,以第二小題為例,處理該問題最簡單的方法是將這個式子解答:
(1)16x²-24xy+9y²
(2)a²+2ab+b²
(二)變項數:
例:計算:(3a+2b+c)²
分析:完全平方公式的左邊是兩個相同的二項式相乘,而本例中出現了三項,故應考慮將其中兩項結合運用整體思想看成一項,從而化解矛盾。所以在運用公式時,(3a+2b+c)²可先變形為[(3a+2b)+c]²,直接套用公式計算。
解答:9a²+12ab+6ac+4b²+4bc+c²
(三)變結構:
例:運用公式計算:
(1)(x+y)(2x+2y)
(2)(a+b)(-a-b)
(3)(a-b)(b-a)
分析:本例中所給的均是二項式乘以二項式,表面看外觀結構不符合公式特征,但仔細觀察易發現,只要將其中一個因式作適當變形就可以了,即
(1)(x+y)(2x+2y)=2(x+y)²
(2) (a+b)(-a-b)=-(a+b)²
(3) (a-b)(b-a)=-(a-b)
歡迎使用手機、平板等移動設備訪問中考網,2025中考一路陪伴同行!>>點擊查看