2023年初中數學一元二次方程高級解題思路

第一講，我們從一元二次方程開始。

中考中，方程的考核有幾個：一元一次、二元一次、一元二次、分式方程、不等式，這其中，最難的也是必考的就是二元一次方程，也是和后續二次函數結合最緊密的考點，所以，今天我們先講。

首先，我們來看一下，初中關于方程和不等式，都學了哪些知識點?下面這些圖，就是這部分知識點的思維導圖。

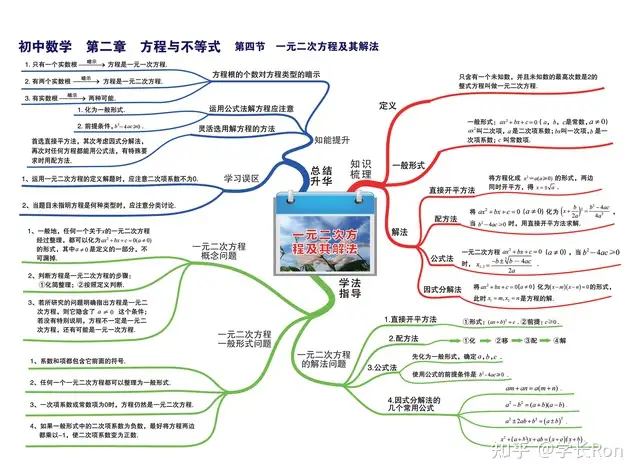
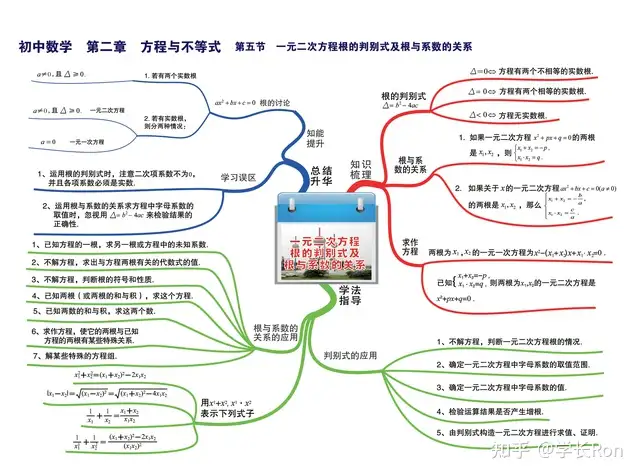
上面兩張圖，包括了初中階段，一元二次方程、不等式的所有知識點，如果同學和孩子還有不知道的點，一定要從書本開始，把基礎的部分打扎實。

第二，我們來講一下一元二次方程在考試中，一般會怎么考?我們該用什么方法來應對。

什么是一元二次方程?

我們把形如

的方程叫一元二次方程。常見的解題方法有以下幾種：配方法、公式法、因式分解法。其中，公式法是解一元二次方程的最普遍、最具有一般性的方法。

為什么說公式法是最普遍，也最具有一般性?

一元二次方程中，常見的判別式“

”，求根公式，包含了初中階段所有學過的代數運算(有分式、有根運算、有冪運算)。同時，它也回答了，求解一元二次方程的諸多問題，比如：怎樣求實根、實根的個數、何時有實根等基本問題……這也是，中考中，常見的幾個考點。

除了上面說的，三種解題方法，還有什么更好用的方法吶?

顯然是有的，告訴大家，解一元二次方程，最基本、最核心的思路就是：降次轉化。

為什么這么說?因為，有些題目中的條件，用公式法運算量很大，甚至在解題過程中，會出現不合理的結果。所以，我們就要想辦法去做一些變形、代換的處理。常用到的降次轉化的方法有：變形降次、整體代入、構造零值多項式等。

下面給大家舉幾個例子：

思路指點：

首先，我們要弄明白基礎概念，什么情況下會等于1?其次，根據不同的情況，求得結果。最后，帶入驗算，和定理、定義對照，是不是符合?

思路指點：

常用的方法，解出這兩個根，發現要用公式法，計算非常繁瑣。那么我們該怎么簡化?這個時候，我們就要想到，降次轉化的基本思路。提示一下，

，同樣，，降次以后，我們的計算是不是變得很簡單。

思路指點：

首先，題目給大家設置了陷阱——“關于x的方程”，沒有說一次，還是二次，你發現了沒?其次，發現了這個陷阱，就會變得簡單，分情況計算，就可以了。

思路指點：

這道題，和上一題一樣，設置了一個陷阱——絕對值。那么，我們就要討論，這個絕對值里面的值是大于等于0，還是小于0?分情況計算，在結合絕對值里面的值是大于等于0，還是小于0，驗算就行了。最后，我們來一個有點難度的。

思路指點：

看上去，這道題很復雜，其實，都是用來干擾你的。出題人，就是要你覺得很復雜，產生一種危難的情緒，然后，放棄掉。

其實，里面是四個等式，然后一個未知數x，其余的啊a,b,c,d，都是常數。我們在解題的時候，就很簡單了，把a,b,c,d，四個常數，用一個來表達替換，比如：b,c,d都用a來表示，就會立馬簡化很多。

最后，我們來總結一下，一元二次方程的變形，主要就是下面的幾種方式。另外，在沒有說明是幾次方程的時候，有絕對值的時候，需要分情況討論、計算。

作業布置：

　　 歡迎使用手機、平板等移動設備訪問中考網，2023中考一路陪伴同行！>>點擊查看