- 全國站
來源：網絡資源 2023-04-09 20:41:14
知識回顧
平面直角坐標系中一個點 P(m，n)
①若向上平移t(t>0)個單位，向y軸正半軸方向平移，橫坐標值不變，縱坐標值變大。平移后的點P1(m，n+t);
②若向下平移t(t>0)個單位，向y軸負半軸方向平移，橫坐標值不變，縱坐標值變笑。平移后的點P2(m，n-t);
③若向右平移t(t>0)個單位，向x軸正半軸方向平移，縱坐標值不變，橫坐標值變大。平移后的點P3(m+t，n);
④若向左平移t(t>0)個單位，向x軸負半軸方向平移，縱坐標值不變，橫坐標值變小。平移后的點P3(m-t，n)
口訣：“上加下減、左減右加”
例題講解
例1：點(2，3)向下平移2個單位再向右平移3個單位，則坐標變為( D )
A.(4，6)B.(0，0)C.(0，6)D.(5，1)
解：原來點的橫坐標是2，縱坐標是3，向下平移2個單位再向右平移3個單位，
得到新點的橫坐標是2+3=5，縱坐標為3﹣2=1.即坐標變為(5，1).
例2：由點A(﹣5，3)到點B(3，﹣5)可以看作( C )平移得到的.
A.先向右平移8個單位，再向上平移8個單位
B.先向左平移8個單位，再向下平移8個單位
C.先向右平移8個單位，再向下平移8個單位
D.先向左平移2個單位，再向上平移2個單位
解：從點A(﹣5，3)到點B(3，﹣5)，橫坐標+8，縱坐標﹣8，故先向右平移8個單位，再向下平移8個單位。
圖形的平移
知識回顧
①圖形平移前后形狀不變，圖形上的點的相對位置也不改變，只有圖形所在的位置改變;
②圖形上每個點平移的路徑是完全一樣的(“平行”且相等);
③平移中，對應點的對應坐標的變化相同，對應坐標的差相等
例題講解
例3：線段CD是由線段AB平移得到的.點A(﹣1，4)的對應點為C(4，7)，則點B(﹣4，﹣1)的對應點D的坐標為( C )
A.(2，9) B.(5，3)
C.(1，2) D.(﹣9，﹣4)
解：平移中，對應點的對應坐標的差相等，設D的坐標為(x，y);根據題意：有4﹣(﹣1)=x﹣(﹣4);7﹣4=y﹣(﹣1)，解可得：x=1，y=2;故D的坐標為(1，2).
例4：△DEF(三角形)是由△ABC平移得到的，點A(﹣1，﹣4)的對應點為D(1，﹣1)，則點B(1，1)的對應點E，點C(﹣1，4)的對應點F的坐標分別為( B )
A.(2，2)，(3，4)
B.(3，4)，(1，7)
C.(﹣2，2)，(1，7)
D.(3，4)，(2，﹣2)
解：點A的對應點D，是橫坐標從﹣1到1，說明是向右移動了1﹣(﹣1)=2個單位，縱坐標是從﹣4到﹣1，說明是向上移動了﹣1﹣(﹣4)=3個單位，那么其余兩點移運轉規律也如此，即橫坐標都加2，縱坐標都加3.故點E、F的坐標為(3，4)、(1，7).故選B.
函數圖象的平移
知識回顧
先回顧下兩直線平移：
若直線y1=k1x+b1與直線y2=k2x+b2平行，那么k1=k2，且b1≠b2
(若k1=k2，且b1=b2，則這兩條直線重合)
知識拓展：斜著平移
二次函數圖象的斜著平移
二次函數圖象的斜著平移在19年重慶中考B卷26題第二問中出現過，最近八中的月考也出現了，如果第一次見到會比較慌張，不知道如何下手，實際上把這個單獨拿出來看，就是一個簡單的平移問題，用函數圖象平移打方法處理就可以了。
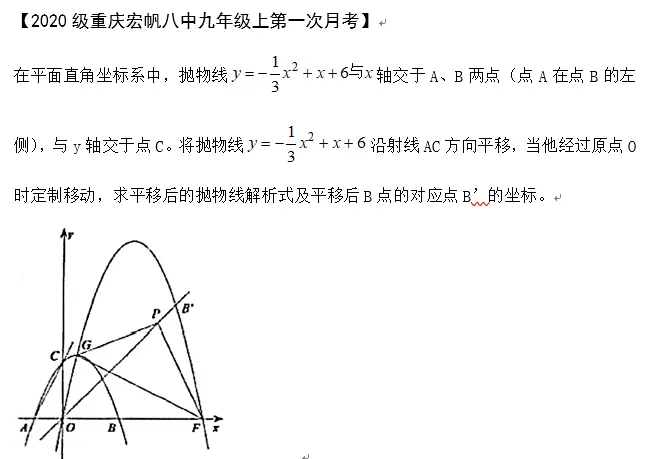
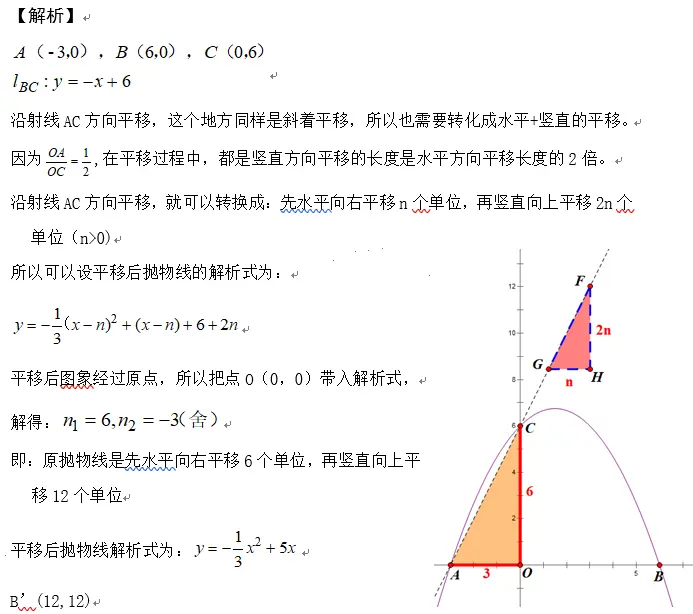
【小結】初中階段，平面直角坐標系中的平移問題就這么多，簡單的就是水平和豎直方向的平移，但是要把點和函數的平移區分開。
斜著平移就轉換成水平+豎直方向的平移，要相信，斜著的平移是一定能轉換成“水平+豎直”的平移的!!!
編輯推薦：
歡迎使用手機、平板等移動設備訪問中考網，2024中考一路陪伴同行！>>點擊查看
