來源:網絡資源 2023-05-30 16:46:26
▊ 三角形兩邊
定理 三角形兩邊的和大于第三邊
推論 三角形兩邊的差小于第三邊
▊ 三角形中位線定理
三角形的中位線平行于第三邊,并且等于它的一半
▊ 三角形的重心
三角形的重心到頂點的距離是它到對邊中點距離的2倍。
在三角形中,連接一個頂點和它對邊中點的線段叫做三角形的中線,三角形的三條中線交于一點,這一點叫做“三角形的重心”。
▊ 與三角形有關的角
1、三角形的內角和定理:三角形的內角和為180°,與三角形的形狀無關。
2、直角三角形兩個銳角的關系:直角三角形的兩個銳角互余(相加為90°)。有兩個角互余的三角形是直角三角形。
3、三角形外角的性質:三角形的一個外角等于與它不相鄰的兩個內角之和;三角形的一個外角大于與它不相鄰的任何一個內角;三角形三個外角和為360°。
▊ 等腰三角形的性質和判定
◆ 性質
1.等腰三角形的兩個底角相等(簡寫成"等邊對等角")。
2.等腰三角形的頂角的平分線,底邊上的中線,底邊上的高重合(簡寫成"等腰三角形的三線合一")。
3.等腰三角形的兩底角的平分線相等(兩條腰上的中線相等,兩條腰上的高相等)。
4.等腰三角形底邊上的垂直平分線到兩條腰的距離相等。
5.等腰三角形的一腰上的高與底邊的夾角等于頂角的一半。
6.等腰三角形底邊上任意一點到兩腰距離之和等于一腰上的高(需用等面積法證明)。
7.等腰三角形是軸對稱圖形,只有一條對稱軸,頂角平分線所在的直線是它的對稱軸,等邊三角形有三條對稱軸。[1]
◆ 判定
在同一三角形中,有兩條邊相等的三角形是等腰三角形(定義)。
在同一三角形中,有兩個角相等的三角形是等腰三角形(簡稱:等角對等邊)
▊ 全等三角形的性質和判定
全等三角形共有5種判定方式:SSS、SAS、ASA、AAS、HL。特殊情況下平移、旋轉、對折也會構成全等三角形。
1、SSS(邊邊邊),即三邊對應相等的兩個三角形全等.
2、SAS(邊角邊),即三角形的其中兩條邊對應相等,且兩條邊的夾角也對應相等的兩個三角形全等.
3、ASA(角邊角),即三角形的其中兩個角對應相等,且兩個角夾的的邊也對應相等的兩個三角形全等.
4、AAS(角角邊),即三角形的其中兩個角對應相等,且對應相等的角所對應的邊也對應相等的兩個三角形全等.
5、HL(斜邊、直角邊),即在直角三角形中一條斜邊和一條直角邊對應相等的兩個直角三角形全等.
注意:
1、SSS、SAS、ASA、AAS可用于任意三角形;HL只限于直角三角形.
2、SSA、AAA不能判定全等三角形.
3、在證明時注意利用定理,如:等式性質、等量代換、等角重合有等角、公共邊、公共角、對頂角相等、等角或同角的余角或補角相等、角平分線定義、線段中點定義等.
4、證明全等寫條件時注意書寫順序.
5、寫全等結論時注意對應頂點的位置.
6、有時全等三角形會結合等腰三角形出現命題.
▊ 直角三角形的判定
判定1:有一個角為90°的三角形是直角三角形。
判定2:若a的平方+b的平方=c的平方,則以a、b、c為邊的三角形是以c為斜邊的直角三角形(勾股定理的逆定理)。
判定3:若一個三角形30°內角所對的邊是某一邊的一半,那么這個三角形是以這條長邊為斜邊的直角三角形。
判定4:兩個銳角互余的三角形是直角三角形。
判定5:證明直角三角形全等時可以利用HL ,兩個三角形的斜邊長對應相等,以及一個直角邊對應相等,則兩直角三角形全等。[定理:斜邊和一條直角對應相等的兩個直角三角形全等。簡稱為HL]
判定6:若兩直線相交且它們的斜率之積互為負倒數,則這兩直線垂直。
判定7:在一個三角形中若它一邊上的中線等于這條中線所在邊的一半,那么這個三角形為直角三角形。
▊ 等邊三角形的判定
⑴三邊相等的三角形是等邊三角形(定義)。
⑵三個內角都相等的三角形是等邊三角形。
⑶有一個角是60度的等腰三角形是等邊三角形。
⑷ 有兩個角等于60度的三角形是等邊三角形。
▊ 勾股定理:
內容:直角三角形兩直角邊的平方和等于斜邊的平方;
表示方法:如果直角三角形的兩直角邊分別為a,b,斜邊為c,那么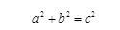
編輯推薦:

歡迎使用手機、平板等移動設備訪問中考網,2025中考一路陪伴同行!>>點擊查看