來源:網絡資源 2023-06-23 18:57:34
1、直角三角形中各元素間的關系
在△ABC中,C=90°,AB=c,AC=b,BC=a。
(1)三邊之間的關系: a² +b²=c²。(勾股定理)
(2)銳角之間的關系:A+B=90°
(3)邊角之間的關系:(銳角三角函數定義)
sinA=cosB=a/c, cosA= sinB=b/c,tanA=a/b。
2、斜三角形中各元素間的關系
在△ABC中,A、B、C為其內角,a、b、c分別表示A、B、C的對邊。
(1)三角形內角和:A+B+C=π 。
(2)正弦定理:在一個三角形中,各邊和它所對角的正弦的比相等。
形式一:a/sinA=b/sinB=c/sinC=2R(R為外接圓半徑)
形式二:a=2RsinA,b=2RsinB,c=2RsinC(邊化正弦)
形式三:a:b:c=sinA:sinB:sinC(比的性質)
形式四:sinA=a/2R,sinB=b/2R,sinC=c/2R(正弦化邊)
(3)余弦定理:三角形任何一邊的平方等于其他兩邊平方的和減去這兩邊與它們夾角的余弦的積的兩倍。
形式一:a²= b²+ c²- 2bccosA;
b²=c²+a² - 2cacosB;
c²=a²+b²- 2abcosC。
形式二:cosA=(b²+ c²-a²)/2bc,
cosB=(a²+ c²-b²)/2ac,
cosC=(a²+b²-c²)/2ab。
3、三角形的面積公式:
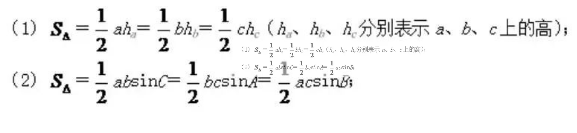
4、解三角形:
由三角形的六個元素(即三條邊和三個內角)中的三個元素(其中至少有一個是邊)求其他未知元素的問題叫做解三角形。廣義地,這里所說的元素還可以包括三角形的高、中線、角平分線以及內切圓半徑、外接圓半徑、面積等等。主要類型:
(1)兩類正弦定理解三角形的問題。
第 1、已知兩角和任意一邊,求其他的兩邊及一角。
第2、已知兩角和其中一邊的對角,求其他邊角。
(2)兩類余弦定理解三角形的問題:
第1、已知三邊求三角。
第2、已知兩邊和他們的夾角,求第三邊和其他兩角。
5、三角形中的三角變換
三角形中的三角變換,除了應用上述公式和上述變換方法外,還要注意三角形自身的特點。
(1)角的變換
因為在△ABC中,A+B+C=π,所以sin( A+B )=sinC; cos(A+B)=-cosC;tan( A+B )=-tanC。

(2)判定三角形形狀時,可利用正余弦定理實現邊角轉化,統一成邊的形式或角的形式。
6、三角形的五心:
垂心一一三角形的三邊上的高相交于一點
重心一一三角形三條中線的相交于一點
外心一一三角形三邊垂直平分線相交于一點
內心一一三角形三內角的平分線相交于一點
旁心一一三角形的一條內角平分線與其他兩個角的外角平分線交于一點
7、三角形誘導公式:
公式一:設α為任意角,終邊相同的角的同一三角函數的值相等。
sin(2kπ+α)=sinα (k∈Z)
cos(2kπ+α)=cosα (k∈Z)
tan(2kπ+α)=tanα (k∈Z)
cot(2kπ+α)=cotα(k∈Z)
公式二:設α為任意角,π+α的三角函數值與α的三角函數值之間的關系。
sin(π+α)= -sinα
cos(π+α)=-cosα
tan(π+α)= tanα
cot(π+α)=cotα
公式三:任意角α與-α的三角函數值之間的關系(利用 原函數 奇偶性)。
sin(-α)=-sinα
cos(-α)= cosα
tan(-α)=-tanα
cot(-α)=-cotα
公式四:利用公式二和公式三可以得到π-α與α的三角函數值之間的關系。
sin(π-α)= sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
公式五利:用公式一和公式三可以得到2π-α與α的三角函數值之間的關系。
sin(2π-α)=-sinα
cos(2π-α)= cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
公式六:π/2±α與α的三角函數值之間的關系。
sin(π/2+α)=cosα
sin(π/2-α)=cosα
cos(π/2+α)=-sinα
cos(π/2-α)=sinα
tan(π/2+α)=-cotα
tan(π/2-α)=cotα
cot(π/2+α)=-tanα
cot(π/2-α)=tanα
8、求解三角形應用題的一般步驟:
(1)分析:分析題意,弄清已知和所求;
(2)建模:將實際問題轉化為數學問題,寫出已知與所求,并畫出示意圖;
(3)求解:正確運用正、余定理求解;
(4)檢驗:檢驗上述所求是否符合實際意義。
編輯推薦:

歡迎使用手機、平板等移動設備訪問中考網,2025中考一路陪伴同行!>>點擊查看