來源:網絡資源 2023-07-22 21:22:06
函數及其圖像
一、平面直角坐標系
1、平面內有公共原點且互相垂直的兩條數軸,構成平面直角坐標系。
在平面直角坐標系內的點和有序實數對之間建立了一一對應的關系。
2、不同位置點的坐標的特征:
3.點P(x,y)坐標的幾何意義:
(1)各象限內點的坐標有如下特征:點P(x,y)在第一象限←→x>0,y>0;點P(x,y)在第二象限←→x<0,y>0;點P(x,y)在第三象限←→x<0,y<0;點P(x,y)在第四象限←→x>0,y<0。(2)坐標軸上的點有如下特征:點P(x,y)在x軸上臺y為0,x為任意實數。點P(x,y)在y軸上一x為0,y為任意實數。(1)點P(x,y)到x軸的距離是∣y∣;(2)點P(x,y)到y袖的距離是∣x∣;(3)點P(x,y)到原點的距離是√(x2+y2)(1)點P(a,b)關于x軸的對稱點是P1(a,-b);(2)點P(a,b)關于y軸的對稱點是P2(-a,b);(3)點P(a,b)關于原點的對稱點是P3(-a,-b);
二、函數的概念
1、常量和變量:
在某一變化過程中可以取不同數值的量叫做變量;保持數值不變的量叫做常量。
2、函數:
一般地,設在某一變化過程中有兩個變量x和y,如果對于x的每一個值,y都有唯一的值與它對應,那么就說x是自變量,y是x的函數。
(1)自變量取值范圍的確是:
①解析式是只含有一個自變量的整式的函數,自變量取值范圍是全體實數。
②解析式是只含有一個自變量的分式的函數,自變量取值范圍是使分母不為0的實數。
③解析式是只含有一個自變量的偶次根式的函數,自變量取值范圍是使被開方數非負的實數。
注意:
在確定函數中自變量的取值范圍時,如果遇到實際問題,還必須使實際問題有意義。
(2)函數值:
給自變量在取值范圍內的一個值所求得的函數的對應值。
(3)函數的表示方法:
①解析法;②列表法;③圖像法
(4)由函數的解析式作函數的圖像,一般步驟是:
①列表;②描點;③連線。
三、幾種特殊的函數
1、一次函數:
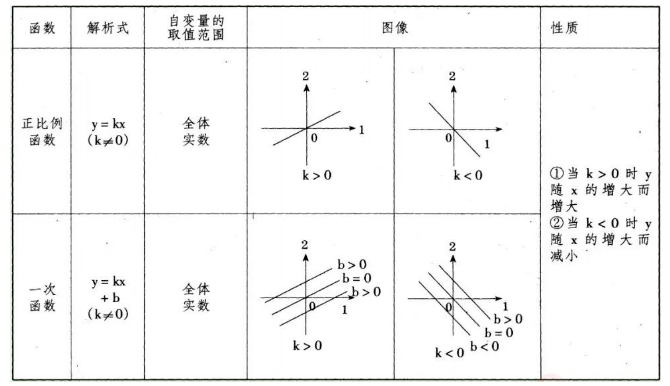
直線位置與k,b的關系:
(1)k>0直線向上的方向與x軸的正方向所形成的夾角為銳角;
(2)k<0直線向上的方向與x軸的正方向所形成的夾角為鈍角;
(3)b>0直線與y軸交點在x軸的上方;
(4)b=0直線過原點;
(5)b<0直線與y軸交點在x軸的下方;
2、二次函數:

拋物線位置與a,b,c的關系:
(1)a決定拋物線的開口方向
a>0←→開口向上;
a<0←→開口向下。
(2)c決定拋物線與y軸交點的位置:
c>0←→圖像與y軸交點在x軸上方;
c=0←→圖像過原點;
c<0←→圖像與y軸交點在x軸下方。
(3)a,b決定拋物線對稱軸的位置:
a,b同號,對稱軸在y軸左側;
b=0,對稱軸是y軸;
a,b異號,對稱軸在y軸右側。
3、反比例函數:
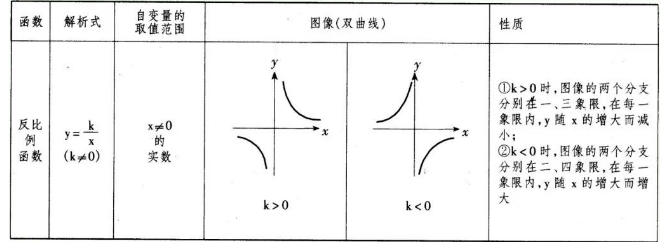
4、正比例函數與反比例函數的對照表:
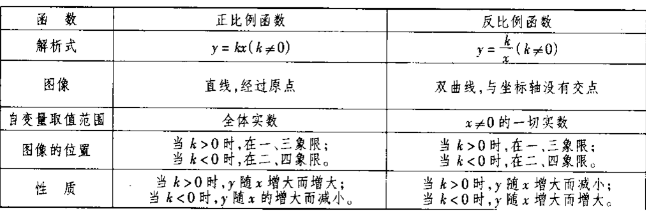
編輯推薦:

歡迎使用手機、平板等移動設備訪問中考網,2025中考一路陪伴同行!>>點擊查看